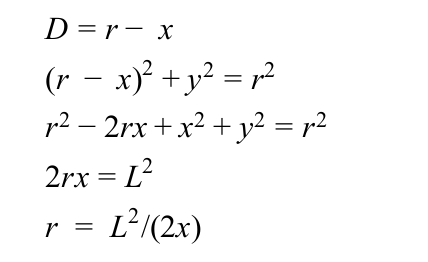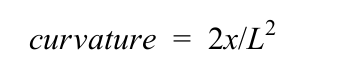算法实现
purepursuit的核心其实是一个曲率半径的几何计算。
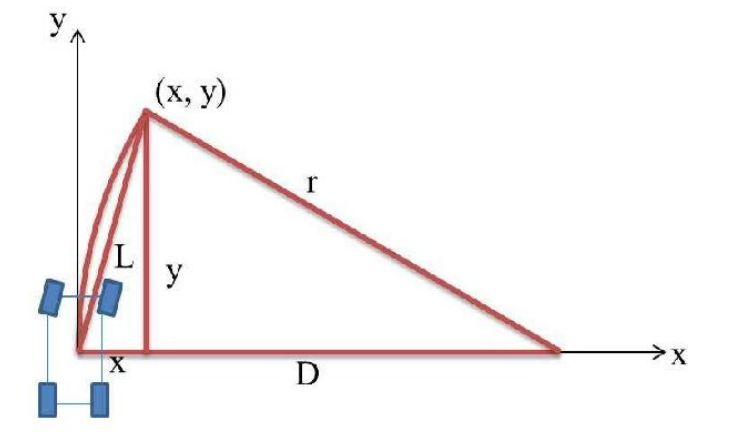
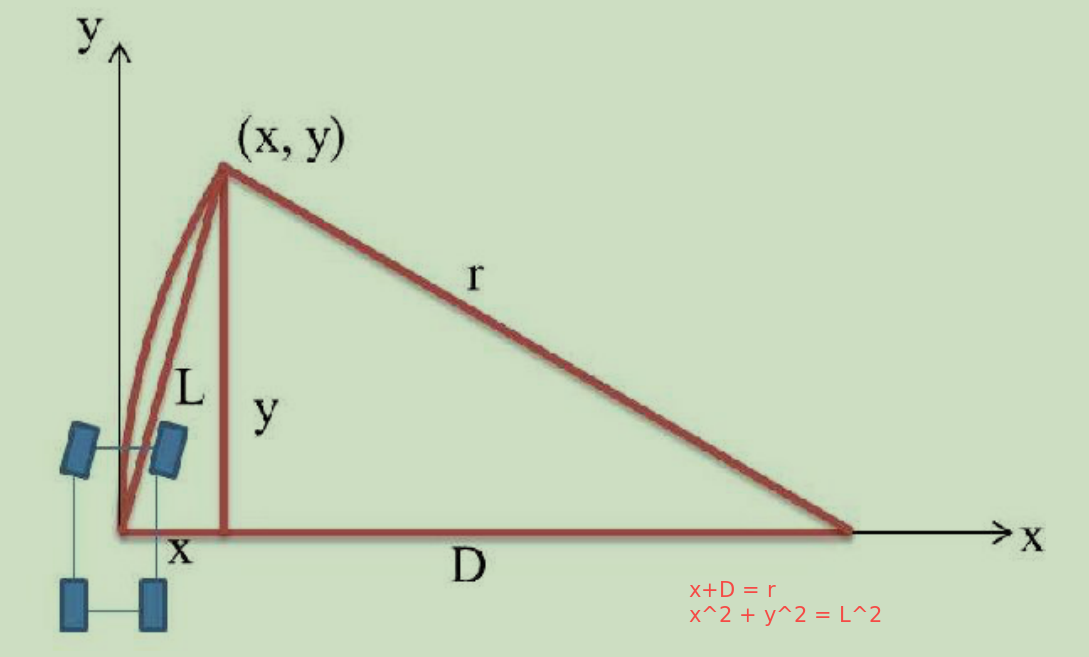
(x, y)是转换到机器人坐标系上的路径点。L是lookahead distance。r是形成的圆弧半径。D是r和x之间的差值。
根据上面的图形,可以发现有下面的几何关系:

同时通过
$$
y^2 + D^2 = r^2
$$
可以推算出下面的等式关系:
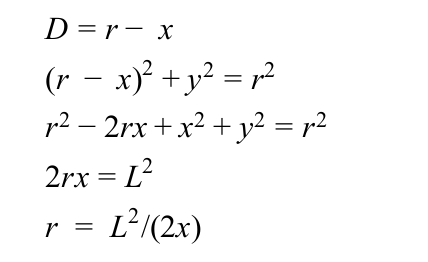
曲率的定义为1 /radius,所以可得到下面的式子:
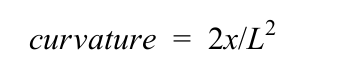
当确定好线速度时,就可以通过下面的方式计算出角速度:
1
| angular_vel = linear_vel * curvature;
|
比较完整的算法描述可参考这篇文档:
https://www.ri.cmu.edu/pub_files/pub3/coulter_r_craig_1992_1/coulter_r_craig_1992_1.pdf
lookahead distance 调整的影响
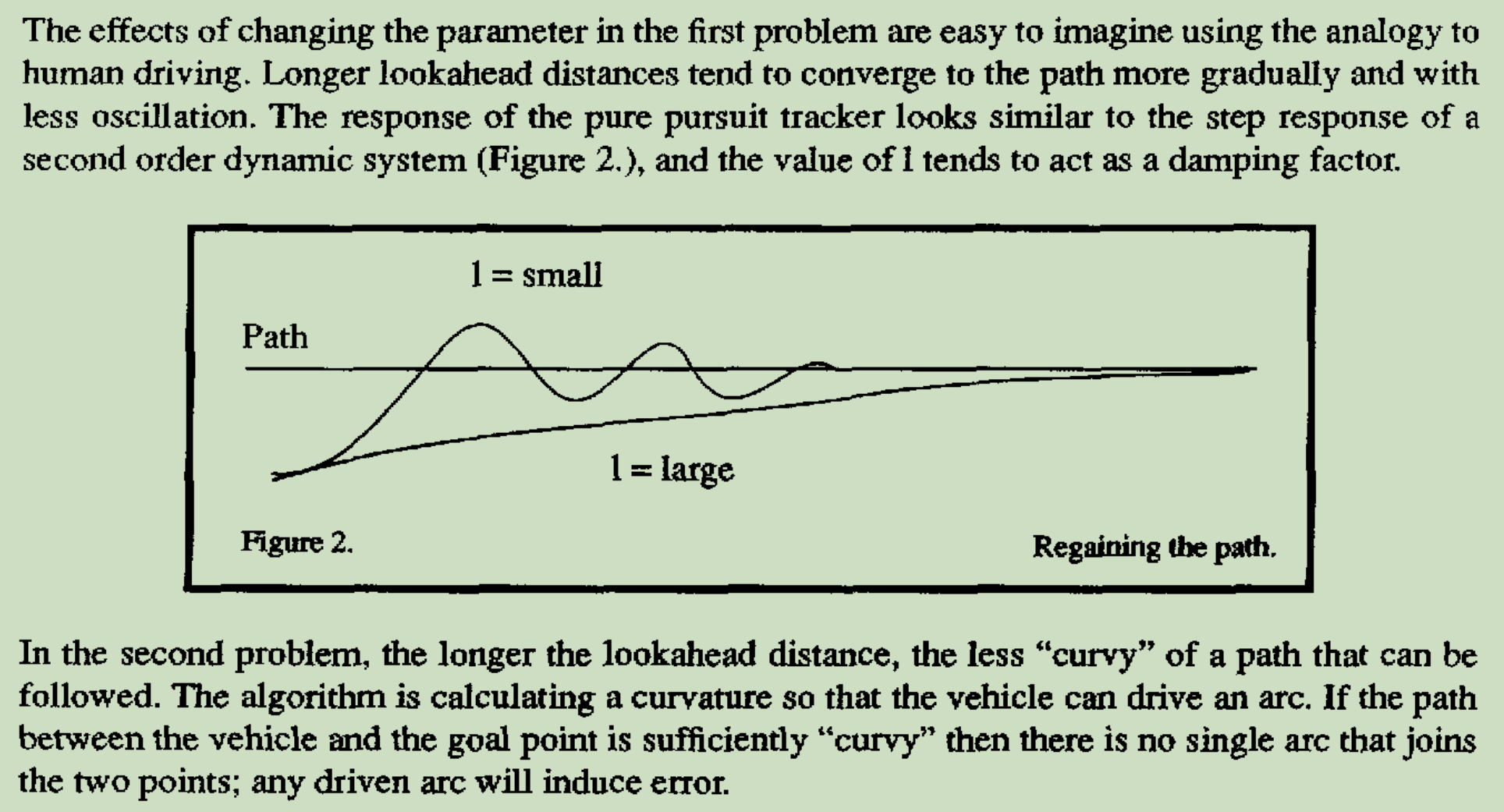
当lookahead_distance值设置的较大时,机器会缓慢贴合到参考路径;
当lookahead_distance值设置的较小时,机器会更快的贴近参考路径。因为没有一个完美的圆弧可以直接让机器贴合到参考路径,所以会产生一些振荡。lookahead_distance值设置的越小,振荡会越大。
没有唯一合适的lookahead_distance
事实上,我们希望针对参考路径的曲率来计算出一个合适的lookahead_distance值。 如果能找到这样一个一一对应关系,我们便可以方便地根据参考路径的曲率设置好lookahead_distance值。
但一个行走圆弧却不能对应唯一的lookahead_distance值。
下图是一个固定曲率的圆形参考路径。在路径上任意取一个目标点计算出的曲率都是一样的。因为无论目标点选在圆弧的何处都可以形成一个等腰三角形,使满足purepursuit的几何关系。
但显然随着目标点的不一样,lookahead_distance值也是不一样的。
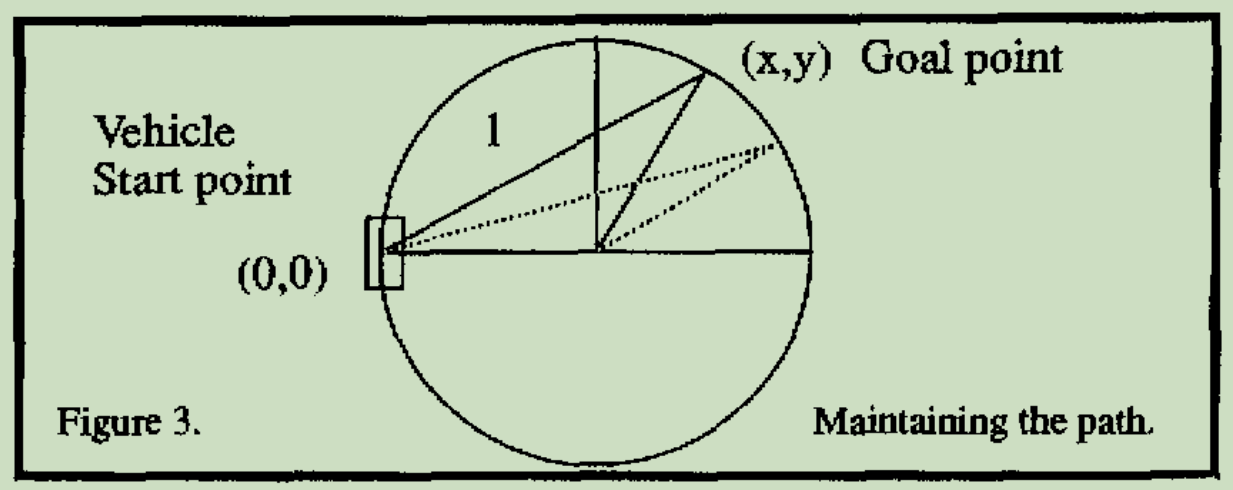
目标点在圆弧的任意一个位置都满足车的行走路径为一个以r为半径的圆弧。事实上,lookahead_distance取0~2r都是可行的。所以,给定一个lookahead_distance值可以得到一个唯一的圆弧半径,但给定一个圆弧半径则不能得到一个唯一的lookahead_distance值。
lookahead_distance 的选取策略
从上面的分析可知,同样的曲率并不对应唯一的lookahead_distance值。但可分析出,如果路径比较弯曲,应该要选取较小的lookahead_distance值,这样才更贴合参考路径;路径比较直时,应该要选取较大的lookahead_distance值。执行速度也有同样的需求,路径比较直的时候可以采用更大的速度,路径比较弯曲时则需减少速度。只有路径特征,执行速度和lookahead_distance值达到一种协调的关系,路径跟随的效果才会比较好。
通过查阅一些相关论文和开源代码,整理了如下策略。
1、计算弯曲半径
根据当前点和当前点前后两点(可间隔)形成一个圆,求取该圆的半径。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
template <typename T>
CircleData findCircle2(const T & pt1, const T & pt2, const T & pt3)
{
float A1, A2, B1, B2, C1, C2, temp;
A1 = pt1.x - pt2.x;
B1 = pt1.y - pt2.y;
C1 = (pow(pt1.x, 2) - pow(pt2.x, 2) + pow(pt1.y, 2) - pow(pt2.y, 2)) / 2;
A2 = pt3.x - pt2.x;
B2 = pt3.y - pt2.y;
C2 = (pow(pt3.x, 2) - pow(pt2.x, 2) + pow(pt3.y, 2) - pow(pt2.y, 2)) / 2;
temp = A1*B2 - A2*B1;
CircleData CD;
if (temp == 0){
CD.center.x = pt1.x;
CD.center.y = pt1.y;
CD.radius = 5.0;
return CD;
}
else{
CD.center.x = (C1*B2 - C2*B1) / temp;
CD.center.y = (A1*C2 - A2*C1) / temp;
}
CD.radius = sqrtf((CD.center.x - pt1.x)*(CD.center.x - pt1.x) + (CD.center.y - pt1.y)*(CD.center.y - pt1.y));
return CD;
}
|
代码来源于:https://blog.csdn.net/lijiayu2015/article/details/52541730/
采用此方法计算整条路径上每个点弯曲半径。
2、设置速度
根据执行路径上距离车体最近的点的弯曲半径来调整车体速度。
可采用如下关系来设置期望速度:
弯曲半径 大于 最大阈值(路径越直弯曲半径越大),设置期望速度为最大速度;
弯曲半径 小于 最小阈值(路径越弯弯曲半径越小),设置期望速度为最小速度;
弯曲半径在最大和最小阈值中间则使用最大速度*调整系数来设置期望速度。 但需确保期望速度不小于最小速度。
限制速度变化率
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
| class RateLimiter {
public:
RateLimiter() = default;
~RateLimiter() = default;
double limitRateOfChange(double value);
void setRisingRate(double maxRisingRate);
void setFallingRate(double minFallingRate);
void setTimestep(double dt);
void reset(double startingValue = 0.0);
private:
double dt_ = 0.01;
double maxRisingRate_ = 1.0;
double minFallingRate_ = -1.0;
double valuePrev_ = 0.0;
};
double RateLimiter::limitRateOfChange(double value) {
double retValue = value;
if (value > valuePrev_ + dt_ * maxRisingRate_) {
retValue = valuePrev_ + dt_ * maxRisingRate_;
}
if (value < valuePrev_ + dt_ * minFallingRate_) {
retValue = valuePrev_ + dt_ * minFallingRate_;
}
valuePrev_ = retValue;
return retValue;
}
void RateLimiter::setRisingRate(double maxRisingRate) {
if (maxRisingRate < 0) {
throw std::runtime_error("Rising rate cannot be negative.");
}
maxRisingRate_ = maxRisingRate;
}
void RateLimiter::setFallingRate(double minFallingRate) {
if (minFallingRate > 0) {
throw std::runtime_error("Falling rate cannot be positive");
}
minFallingRate_ = minFallingRate;
}
void RateLimiter::setTimestep(double dt) {
if (dt < 0) {
throw std::runtime_error("Time step cannot be negative");
}
dt_ = dt;
}
void RateLimiter::reset(double startingValue) {
valuePrev_ = startingValue;
}
|
开源代码来源于:https://github.com/leggedrobotics/se2_navigation.git
处理接近终点的情况。速度还需根据距离终点的距离线性调整。参考开源代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| bool AdaptiveVelocityController::computeVelocity() {
double referenceVelocity = 0.0;
switch (drivingDirection_) {
case DrivingDirection::FWD: {
referenceVelocity = parameters_.desiredVelocity_;
break;
}
case DrivingDirection::BCK: {
referenceVelocity = -parameters_.desiredVelocity_;
break;
}
}
const double distanceToGoal = (currentRobotState_.pose_.position_ - currentPathSegment_.point_.back().position_).norm();
const double dWhenBrakingStarts = parameters_.distanceToGoalWhenBrakingStarts_;
if (distanceToGoal <= dWhenBrakingStarts) {
const double slope = parameters_.desiredVelocity_ / dWhenBrakingStarts;
const double referenceVelocityMagnitude = slope * distanceToGoal;
const double direction = sgn(referenceVelocity);
referenceVelocity = direction * referenceVelocityMagnitude;
}
desiredLongitudinalVelocity_ = rateLimiter_.limitRateOfChange(referenceVelocity);
return true;
}
|
3、设置lookahead_distance值
根据Real-time Motion Planning with Applications to Autonomous Urban Driving这篇论文中提到的方法。这里根据上面输出的期望速度来调整lookahead_distance值。


上图的比例关系是论文中针对乘用车设置的。在实际工程项目中应该还需要根据实际情况调整。
4、适时进行原地旋转
通过lookahead_distance值选取lookahead point。计算lookahead point相对于机器人位置的朝向与机器人朝向的差值,如果差值太大就进行原地旋转。